Inputs and Parameters
Differential equations may also contain not only state variables, but also parameters and input functions. For instance, consider the system:
where \(c_1, c_2 \in \mathbb{C}\) are parameters and \(u(t)\) is an unknown input function.
In QBee we introduce them in the following way:
>>> from qbee import *
>>> c1, c2 = parameters("c1, c2")
>>> x, y, u = functions("x, y, u")
>>> system = [(x, c1*y*u), (y, c2*x**3)] # u is considered as input since it's not in the left-hand side;
>>> quadratize(system).print()
Introduced variables:
w0 = x**2
w1 = x*y
w2 = y**2
x' = c1*u*y
y' = c2*w0*x
w0' = 2*c1*u*w1
w1' = c1*u*w2 + c2*w0**2
w2' = 2*c2*w0*w1
Inputs’ Derivatives
Note that we can introduce a derivative of an input function during quadratization. Let’s look at this with an example:
>>> from qbee import *
>>> x, y, u = functions("x, y, u")
>>> system = [(x, y**2 * u), (y, x**2)]
>>> quadratize(system).print()
Introduced variables:
w0 = u*y
w1 = u*x
x' = w0*y
y' = x**2
w0' = u'*y + w1*x
w1' = u'*x + w0**2
It should be mentioned that sometimes the derivatives of the input functions are unknown or do not even exist! To cover such cases, we can try to find an input-free quadratization, i.e. quadratization contains no input functions and therefore does not introduce their derivatives.
>>> from qbee import *
>>> x, y, u = functions("x, y, u")
>>> system = [(x, y**2 * u), (y, x**2)]
>>> quadratize(system, input_free=True).print()
Introduced variables:
w0 = y**2
w1 = x**2
w2 = x*y**2
w3 = x*y
w4 = y**3
w5 = y**4
x' = u*w0
y' = w1
w0' = 2*w1*y
w1' = 2*u*w2
w2' = u*w5 + 2*w1*w3
w3' = u*w4 + w1*x
w4' = 3*w3**2
w5' = 4*w2*w3
It is clear that the order of quadratization in the input-free case has increased significantly. This is not accidental: such quadratizations are indeed larger and do not even always exist!
Existence of input-free quadratizations
The existence from problem of input-free quadratization is thoroughly discussed in Section 3.2 of Exact and optimal quadratization of nonlinear finite-dimensional non-autonomous dynamical systems . Here, however, we will only give our results and helpful practices.
Consider original system to be input-affine, that is, of the form
Theorem 1: if the system (1) is also a polynomial-bilinear, that is, the total degree of \(\mathbf{p_i}(\mathbf{x})\) is at most one for every \(1 \le i \le r\), then there is an input-free quadratization.
It turns out that the existence of input-free quadratization can be characterized via the properties of certain linear differential operators associated with inputs \(\mathbf{u}(t)\).
Definition 1: We introduce \(r\) differential operators for the system (1):
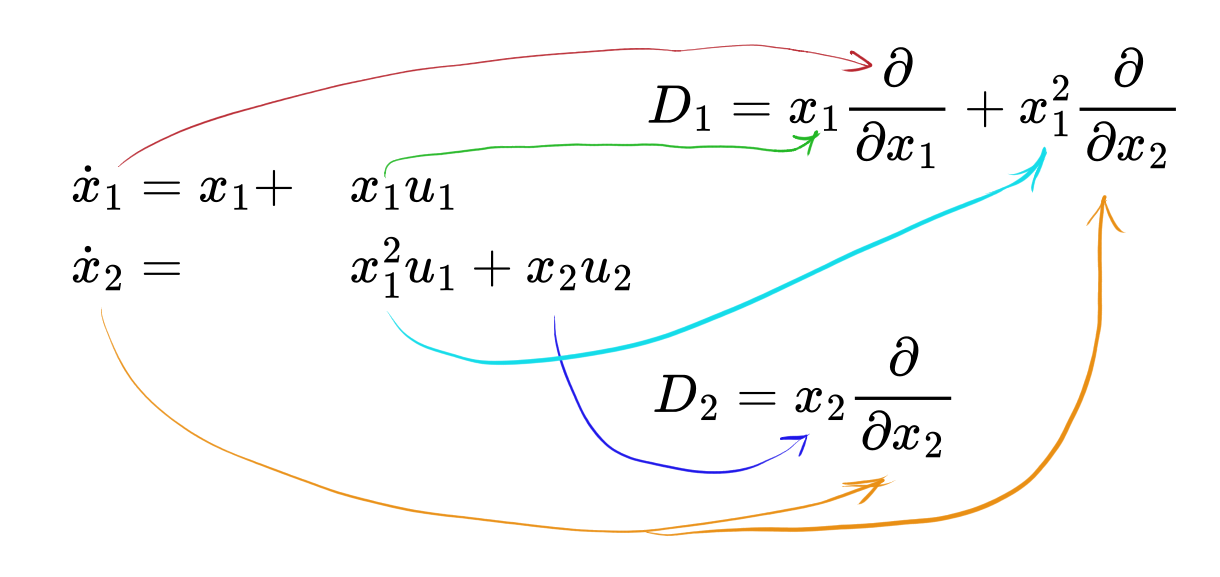
It is easier to imagine with an example. Consider the following system:
Then we introduce two differential operators \(D_1\) and \(D_2\), associated with \(u_1\) and \(u_2\) accordingly:
Below you can see how we build up these operators more visually:
Theorem 2: Let \(\mathcal{A}\) be a subalgebrra generated by \(D_1,\dots, D_r\) in the algebra \(\mathbb{C}[\mathbf{x}, \mathbf{\frac{\partial}{\partial x}}]\) of all polynomial differential operators in \(\mathbf{x}\). Then there is an input-free quadratization of (1) if and only if
Let’s use the example above to show how the theorem works.
For \(x_1\) we have
For \(x_2\) we have
Therefore, Theorem 2 implies that the example system has an input-free quadratization. And indeed:
>>> x1, x2, u1, u2 = functions("x1, x2, u1, u2")
>>> system = [(x1, x1 + x1 * u1), (x2, x1**2 * u1 + x2 * u2)]
>>> quadratize(system, input_free=True).print()
Introduced variables:
w0 = x1**2
x1' = u1*x1 + x1
x2' = u1*w0 + u2*x2
w0' = 2*u1*w0 + 2*w0
Now consider an example where there is no input-free quadratization.
Associated differential operator is \(D = x^2 \frac{\partial}{\partial x}\) and the algebra \(\mathcal{A}\) spanned by
>>> x, u = functions("x, u")
>>> system = [(x, x**2 * u)]
>>> upper_bound = partial(pruning_by_vars_number, nvars=100) # Max quadratization order = 100
>>> res = quadratize(system, input_free=True, pruning_functions=[upper_bound, *default_pruning_rules])
>>> print(res)
None
Why Theorem 2 is not in QBee yet
The problem is that a complete algorithm for solving this kind of problem has not yet been found in the general case (See Remark 3.10 of the article above). For the input-free quadratization problem specifically, there is some progress, but we have not yet been able to fully prove the correctness of the proposed algorithm.
Setting up possible derivatives of inputs
Sometimes there are cases where input-free quadratizations are not required and you know exactly how many derivatives your input functions have.
You can use the input_ders_order parameter to denote
the maximum allowed order of derivatives for input functions.
>>> x, y, u, v = functions("x, y, u, v")
>>> system = [(x, y**2 * u), (y, v * x**2)]
>>> quadratize(system, input_der_orders={v: 2, u: 0}).print() # v' and v'' are allowed
Introduced variables:
w0 = y**2
w1 = v*x
w2 = v*y**2
w3 = v*x*y
w4 = v'*x
w5 = v'*y**2
w6 = v*x**2
w7 = v*y**3
w8 = v*x*y**2
w9 = v*y**4
x' = u*w0
y' = w6
w0' = 2*w6*y
w1' = u*w2 + w4
w2' = 2*w1*w3 + w5
w3' = u*w7 + w1*w6 + w4*y
w4' = u*w5 + v''*x
w5' = v''*w0 + 2*w3*w4
w6' = 2*u*w8 + w4*x
w7' = 3*w3**2 + w5*y
w8' = u*w9 + w0*w4 + 2*w3*w6
w9' = w0*w5 + 4*w6*w7